[ Chapter start ] [ Previous page ] [ Next page ]

---

17.1.1  Goals and Objectives

The input to the global router is a floorplan that includes the locations of all the fixed and flexible blocks; the placement information for flexible blocks; and the locations of all the logic cells. The goal of global routing is to provide complete instructions to the detailed router on where to route every net. The objectives of global routing are one or more of the following:

• Minimize the total interconnect length.
• Maximize the probability that the detailed router can complete the routing.
• Minimize the critical path delay.

In both floorplanning and placement, with minimum interconnect length as an objective, it is necessary to find the shortest total path length connecting a set of terminals . This path is the MRST, which is hard to find. The alternative, for both floorplanning and placement, is to use simple approximations to the length of the MRST (usually the half-perimeter measure). Floorplanning and placement both assume that interconnect may be put anywhere on a rectangular grid, since at this point nets have not been assigned to the channels, but the global router must use the wiring channels and find the actual path. Often the global router needs to find a path that minimizes the delay between two terminals—this is not necessarily the same as finding the shortest total path length for a set of terminals.

17.1.2  Measurement of Interconnect Delay

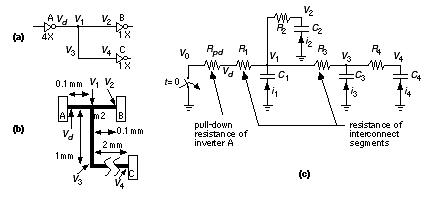
Floorplanning and placement need a fast and easy way to estimate the interconnect delay in order to evaluate each trial placement; often this is a predefined look-up table. After placement, the logic cell positions are fixed and the global router can afford to use better estimates of the interconnect delay. To illustrate one method, we shall use the Elmore constant to estimate the interconnect delay for the circuit shown in Figure 17.3 .

FIGURE 17.3  Measuring the delay of a net. (a) A simple circuit with an inverter A driving a net with a fanout of two. Voltages V 1 , V 2 , V 3 , and V 4 are the voltages at intermediate points along the net. (b) The layout showing the net segments (pieces of interconnect). (c) The RC model with each segment replaced by a capacitance and resistance. The ideal switch and pull-down resistance R pd model the inverter A.

The problem is to find the voltages at the inputs to logic cells B and C taking into account the parasitic resistance and capacitance of the metal interconnect. Figure 17.3 (c) models logic cell A as an ideal switch with a pull-down resistance equal to R _pd and models the metal interconnect using resistors and capacitors for each segment of the interconnect.

The Elmore constant for node 4 (labeled V ₄ ) in the network shown in Figure 17.3 (c) is

		4
t D 4	=	S	R k 4 C k		(17.1)
		k = 1
	=	R 14 C 1 + R 24 C 2 + R 34 C 3 + R 44 C 4 ,

where,

R 14	=	R pd + R 1		(17.2)
R 24	=	R pd + R 1
R 34	=	R pd + R 1 + R 3
R 44	=	R pd + R 1 + R 3 + R 4

In Eq.  17.2 notice that R ₂₄ = R _pd + R ₁ (and not R _pd + R ₁ + R ₂ ) because R ₁ is the resistance to V ₀ (ground) shared by node 2 and node 4.

Suppose we have the following parameters (from the generic 0.5 m m CMOS process, G5) for the layout shown in Figure 17.3 (b):

• m2 resistance is 50 m W /square.
• m2 capacitance (for a minimum-width line) is 0.2 pFmm ^–1 .
• 4X inverter delay is 0.02 ns + 0.5 C _L ns ( C _L is in picofarads).
• Delay is measured using 0.35/0.65 output trip points.
• m2 minimum width is 3 l = 0.9 m m.
• 1X inverter input capacitance is 0.02 pF (a standard load).

First we need to find the pull-down resistance, R _pd , of the 4X inverter. If we model the gate with a linear pull-down resistor, R _pd , driving a load C _L , the output waveform is exp – t /( C _L R _pd ) (normalized to 1V). The output reaches 63 percent of its final value when t = C _L R _pd , because exp (–1) = 0.63. Then, because the delay is measured with a 0.65 trip point, the constant 0.5 nspF ^–1 = 0.5 k W is very close to the equivalent pull-down resistance. Thus, R _pd ª 500 W .

From the given data, we can calculate the R ’s and C ’s:

		(0.1 mm) (50 ¥ 10 –3 W )
R 1 = R 2	=	––––––––––––––––––––	=	6 W
		0.9 m m
		(1 mm) (50 ¥ 10 –3 W )
R 3	=	––––––––––––––––––––	=	56 W
		0.9 m m
		(2 mm) (50 ¥ 10 –3 W )
R 4	=	––––––––––––––––––––	=	112 W
		0.9 m m
					(17.3)

C 1	=	(0.1 mm) (0.2 ¥ pFmm –1 )	=	0.02 pF
C 2	=	(0.1 mm) (0.2 ¥ pFmm –1 ) + 0.02 pF	=	0.04 pF
C 3	=	(1 mm) (0.2 ¥ pFmm –1 )	=	0.2 pF
C 4	=	(2 mm) (0.2 ¥ pFmm –1 ) + 0.02 pF	=	0.42 pF
					(17.4)

Now we can calculate the path resistance, R _ki , values (notice that R _ki = R _ik ):

R 14	=	500 W + 6 W	=	506 W
R 24	=	500 W + 6 W	=	506 W
R 34	=	500 W + 6 W + 56 W	=	562 W
R 44	=	500 W + 6 W + 56 W + 112 W	=	674 W
					(17.5)

Finally, we can calculate Elmore’s constants for node 4 and node 2 as follows:

t D 4	=	R 14 C 1 + R 24 C 2 + R 34 C 3 + R 44 C 4			(17.6)
	=	(506)(0.02) + (506)(0.04)
		+ (562)(0.2) + (674)(0.42)
	=	425 ps .

t D 2	=	R 12 C 1 + R 22 C 2 + R 32 C 3 + R 42 C 4			(17.7)
	=	( R pd + R 1 )( C 2 + C 3 + C 4 )
		+ ( R pd + R 1 + R 2 ) C 2
	=	(500 + 6 + 6)(0.04)
		+ (500 + 6)(0.02 + 0.2 + 0.2)